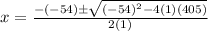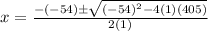)Given:
The length of the wire is 6 meters longer than the height of the tree.
The distance between the anchored point of the wire and the base of the tree is 21 meters shorter than the height of the tree.
Aim:
We need to find the height of the tree,
Step-by-step explanation:
Let h be the height of the tree.
The length of the wire = h+6.
The distance between the anchored point of the wire and the base of the tree = h-21.
Use the Pythagorean theorem.
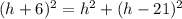
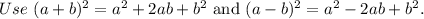
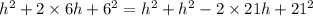
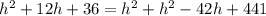
Solve for h.
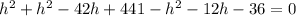
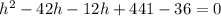
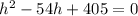
Which is of the form

where a=1, b=-54 and c=405.
Consider the quadratic formula.
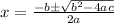
Raplace x=h, a=1, b=-54 and c=405 in the equaiton to find the valaue of h.