Question

I dont understand the thing with the parallel lines and the perpendicular

Answer 1

Given;

`\begin{gathered} \bar{AD}\perp\bar{DB} \\ \bar{DB}\perp\bar{BC} \\ \bar{AB}\cong\bar{CD} \end{gathered}`

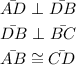
Line AD is perpendicular to line DB, line DB is perpendicular to line BC and line AB is congruent to line CD.

To prove that line AB is perpendicular to line DC, we have to establish that the alternate angles ABD and BDC are congruent.

`\angle ABD\cong\angle BDC`

From congruent triangles, we know that when two triangles have two congruent sides (Hypothenuse and a side) and both have a right angle then they are congruent (RHS - Right angle Hypothenuse Side).

For Triangle ADB and triangle CBD,

The sides AD and CB are congruent, and also side DB is congruent to BD.

`\begin{gathered} \bar{AB}\cong\bar{CD}\text{ ----Hypothenuse} \\ \bar{DB}\cong\bar{BD}\text{ -----side} \\ \angle ADB\cong\angle CBD\cong90^{0\text{ }}-----Right\text{ angle} \end{gathered}`

Therefore, triangle ADB and triangle CBD are congruent.

So, corresponding sides and angles of the two congruent triangles are also congruent.

`\begin{gathered} \bar{AD}\cong\bar{BC} \\ \angle ABD\cong\angle BDC \end{gathered}`

Therefore, since the alternate angles ABD and BDC then line AB is parallel to DC.

`\bar{AB}\parallel\bar{DC}`

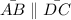
Reason: Alternate interior angles.

If two lines are cut by a transversal and the alternate interior angles are equal (or congruent), then the two lines are parallel.