Question

An ant is located half a meter from the bottom of a wall. When she aims the top of the wall, the angle of inclination becomes 60 °. Calculate the height of the wall H.

Answer 1

Given:

Distance from ant to bottom of the wall = 0.5 meter

Angle of inclination = 60 degrees

Let's find the height of the wall, H.

Let's sketch a figure which represents this situation:

Let's find the height, h.

To find the height, h , apply the trigonometric ratio for tangent:

`tan\theta=(opposite)/(adjacent)`

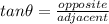
Where:

Opposite side is the side opposite the angle = height if wall, H

adjacent side is the side adjacent the angle = 0.5 meters

θ is the angle = 60 degrees

Plug in the values and solve for H:

`\begin{gathered} tan60=(H)/(0.5) \\ \\ \text{ Multiply both sides by 0.5} \\ \\ 0.5tan60=(H)/(0.5)*0.5 \\ \\ 0.87=H \\ \\ H=0.87\text{ m} \end{gathered}`

Therefore, the height of the wall, H is 0.87 meters.

ANSWER:

0.87 meters