using the definition of secant we know that,
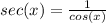
then, the definition of x-intercept is that the function evaluated is equal to 0 then, if f(x) is equal to cos(x)
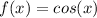
we can say that if the function is equal to 0 then the function secant will look something like this
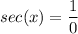
and we know that any number divided by 0 is undefined, so the x.intercepts make the function secant undefined, meaning that the x-intercepts become vertical asymptotes in the secant function.
Answer:
The x-intercepts of the function cosine become the vertical asymptotes of the secant function.