Question

Classifying parallelograms in the coordinate planePart A: Slope of RSSlope of side adjacent to RSPart B: Length of RSLength of side adjacent to RSFrom parts (a) and (b), what can we conclude about parallelogramPORS? Check all that apply.O PORS is a rectangle.O PQRS is a rhombus.O PQRS is a square.- PORS is none of these.

Answer 1

Given:

PQRS has vertices P(6, -6), Q(1, 1), R(-6, 6) and S(-1, -1)

Required: Complete each part

Step-by-step explanation:

Part A:

By using the two point formula,

`\begin{gathered} \text{ Slope of RS =}(-1-6)/(-1-(-6)) \\ =-(7)/(5) \end{gathered}`

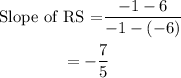
Sides adjacent to RS are RQ ans SP.

Slope of RQ

`\begin{gathered} =(6-1)/(-6-1) \\ =-(5)/(7) \end{gathered}`

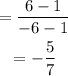
Part B:

Length of RS

`\begin{gathered} =√((-6-(-1))^2+(6-(-1))^2) \\ =√(25+49) \\ =√(74) \end{gathered}`

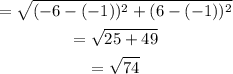
Length of side adjacent to RS

`\begin{gathered} RQ=√((-6-1)^2+(6-1)^2) \\ =√(49+25) \\ =√(74) \end{gathered}`

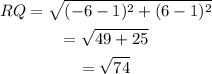
(c) It is a parallelogram with all sides equal. Hence it is a rhombus.

Final Answer: