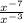Answer::
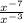
Explanation:
Given the expression:
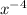
We want to find an expression that simplifies to the given expression.
Consider the expression below:
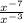
Applying the division law of indices:
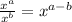
Therefore:
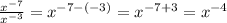
An expression that simplifies to the given expression is: