Question

An envelope measures 8 inches by 5 inches. A pencil is placed in the envelope at a diagonal. What is the maximum possible length of the pencil? If necessary, round to the nearest tenth.

Answer 1

`9.4in`

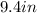
Step-by-step explanation

First, let us make a sketch of the problem:

The envelope is shaped like a rectangle.

The maximum possible length of the pencil is the length of the diagonal of the envelope.

To find the length of the diagonal, apply the Pythagoras theorem:

`\text{hyp}^2=a^2+b^2`

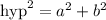
where hyp = hypotenuse

a, b = legs of the triangle formed by the diagonals and the sides of the envelope.

Therefore, for the question, we have that:

`\begin{gathered} p^2=5^2+8^2 \\ p^2=25+64 \\ p^2=89 \\ p=\sqrt[]{89} \\ p\approx9.4in \end{gathered}`

The maximum possible length of the pencil is 9.4 inches.