First, we have that the equation to calculate the reflection over the x-axis is:
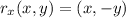
And the forumal for the reflection of point 'a' across the point 'p' is:

then, for the point C(-1,3), we have the following:
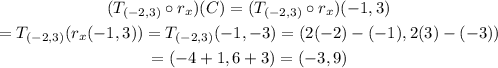
therefore, the image of C(-1,3) under the transformations is (-3,9)