Question

If a sphere fits snugly inside a cube with 34-in edges. What’s is the approximate volume of the space between the sphere and cube

Answer 1

The volume of the space between the sphere and cube is equal to the volume of the sphere subtracted from the volume of the cube:

`V_{}=V_(cube)-V_(sphere)`

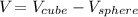
The volume of a cube is:

`V=s^3`

s is the length of each edge in the cube

The volume of a sphere is:

`V=(4)/(3)\pi\cdot r^3`

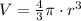
The diameter of the sphere is equal to the edge of the cube, then, its radiusr is:

`r=(s)/(2)`

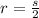
Then, the volume of the space between the sphere and cube is:

`V=s^3-(4)/(3)\pi\cdot((s)/(2))^3`

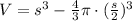
s is 34 in

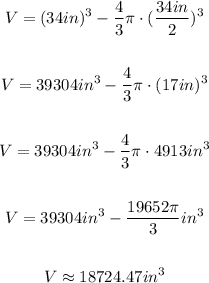
`\begin{gathered} V=(34in)^3-(4)/(3)\pi\cdot((34in)/(2))^3 \\ \\ V=39304in^3-(4)/(3)\pi\cdot(17in)^3 \\ \\ V=39304in^3-(4)/(3)\pi\cdot4913in^3 \\ \\ V=39304in^3-(19652\pi)/(3)in^3 \\ \\ V\approx18724.47in^3 \end{gathered}`Then, the approximate volume of the space between the sphere and cube is 18724,47 cubic inches