5. State the null and the alternate hypothesis.
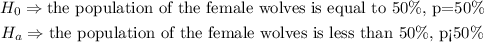
Given an alpha of 0.01, the level of significance will

A left tailed test will be used, because we want to nullify that the population is less than 50%
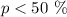
6. The z-test statistic and the P-value will be
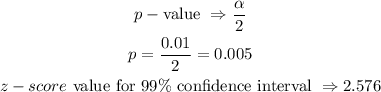
8. Since the p-value is less than the alpha value, then, we will reject the null hypothesis in favour of the alternative hypothesis.
Yes, the data are statistically significant at the level of alpha
We conclude that the population of the female wolves is less than 50%