Question

A theatre group made appearances in two cities. The hotel charge before tax in the second city was $1500 lower than the first. The tax in the first city was 5% and the tax in the second city was 7%. The hotel tax paid for the two cities was $435. How much was the hotel charge in each city before tax?

Answer 1

Data:

City 1: A

City 2: B

Tax (r):

B= 7%

A=5%

`\begin{gathered} A=C_A+C_A(0.05) \\ B=C_B+C_B(0.07) \end{gathered}`

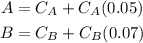
Cost without tax: C

Tax: C( r %)

The hotel charge before tax in the second city was $1500 lower than the first:

`C_B=C_A-1500`

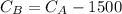
The hotel tax paid for the two cities was $435:

`C_A(0.05)+C_B(0.07)=435`

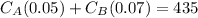
Use the equations above to find the hotel charge (CA and CB) in each city:

1. Substitute in the second equation the CB for the value of CB in the first equation:

`C_A(0.05)+(C_A-1500)(0.07)=435`

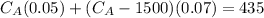
2. Solve CA:

`\begin{gathered} \text{0}.05C_A+0.07C_A-105=435 \\ \\ 0.12C_A-105=435 \\ \\ 0.12C_A=435+105 \\ \\ 0.12C_A=540 \\ \\ C_A=(540)/(0.12) \\ \\ C_A=4500 \end{gathered}`

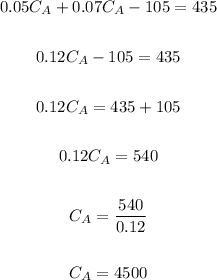
3. Use the value you find for CA to find CB:

`\begin{gathered} C_B=C_A-1500 \\ C_B=4500-1500 \\ \\ C_B=3000 \end{gathered}`

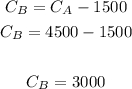
Then, the charge before tax of the hotel in first city (CA) is $4500 and in the second hotel (CB) is $3000