First, let's find a function that will give us the area with for the dimensions.
Since the area is rectangular, let two sides be x and the other be y:
This means that the sum of these three sides have to be equal to 1000 meters:
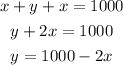
Also, the area of the rectangle is:
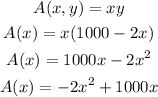
This is a quadratic function and, since its leading coefficient is negative, it has a maximum value at its vertex. The x value of the vertex corresponds to the x variable of the function, and the y value corresponds to the maximum value of the function A(x).
The x coordinate of the vertex of a quadratic function is:
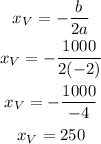
So, the value of x for which the field has maximum area is 250, which means that the other side of the field is:
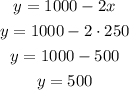
So, the field will have maximum area when its dimensions are 250 meter x 500 meters.
The y value of the vertex can be calculated inputting the x value into the funciton, so:
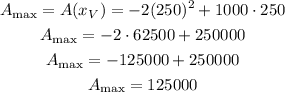
So, the maximum are of the field will be 125000 squared meters.