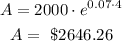Question

Question 29. Find the amount A, in a savings account is $2000 is invested at 7% for 4 years and the interest is compounded:

Answer 1

The compound interest formula is given by

`A=P(1+(r)/(n))^(n\cdot t)`

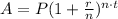
where A is the resulting amount, P is the amount of principal, r is the annual interest rate, n is the number of compounding periods per year and t is the time in years.

In our case, r=0.07, P=$2000 and t=4 years. The number of compounding periods n depends on the given case:

Part A. Annually.

In this case, n= 1 . Then, the resulting amount A is

`A=2000(1+(0.07)/(1))^(1\cdot4)`

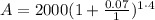
which gives

`\begin{gathered} A=2000(1.07)^(1\cdot4) \\ A=\text{ \$}2621.59 \end{gathered}`

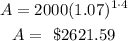
Part B. Semuannually.

In this case, n=2 (twice per year). Then, the resulting amount A is

`\begin{gathered} A=2000(1+(0.07)/(2))^(2\cdot4) \\ A=2000(1.035)^8 \\ A=\text{ \$}2633.62 \end{gathered}`

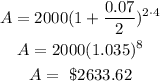
Part C. Quarterly.

In this case, n=4 (4 times per year). So, the resulting amount A is

`\begin{gathered} A=2000(1+(0.07)/(4))^(4\cdot4) \\ A=2000(1.0175)^(16) \\ A=\text{ \$}2639.86 \end{gathered}`

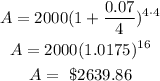
Part D. Daily.

In this case, n= 360 (360 times per year). Then, the resulting amount A is

`\begin{gathered} A=2000(1+(0.07)/(360))^(360\cdot4) \\ A=2000(1.0001944)^(360\cdot4) \\ A=\text{ \$ }2646.19 \end{gathered}`

Part E. Continuosly.

In this case, our first formula becomes

`A=P\cdot e^(r\cdot t)`

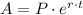
then, by substituting our given values, we have

`\begin{gathered} A=2000\cdot e^(0.07\cdot4) \\ A=\text{ \$2646.26} \end{gathered}`