Question

A town's population is currently 20,950. If the population doubles every 92 years, what will the population be 460 years from now?

Answer 1

We have an exponential growth problem here, it is given by the formula:

`P(t)=P(0)\cdot e^(kt)`

Where t is the time in years, P(0) is the initial population at t=0, and k is a constant.

We already know the population at t=0: P(0)=20,950.

And it doubles every 92 years, then when t=92, P(92)=2*P(0).

If we replace these values we can solve for k as follows:

`\begin{gathered} P(0)=20,950\cdot e^(k\cdot0)=20,950 \\ P(92)=2\cdot20,950=41,900=20,950\cdot e^(k\cdot92) \\ We\text{ can solve for k as follows} \\ 41,900=20,950\cdot e^(k\cdot92) \\ (41,900)/(20,950)=e^(k\cdot92) \\ 2=e^(k\cdot92) \\ \text{Apply ln to both sides} \\ \ln 2=\ln e^(k\cdot92) \\ \text{Apply the properties of logarithms:} \\ 0.693=k\cdot92\cdot\ln e \\ \text{Simplify} \\ 0.693=k\cdot92 \\ k=(0.693)/(92) \\ k=0.0075 \end{gathered}`

Then, to know the population 460 years from now, we need to replace k=0.0075 and t=460 and solve:

`\begin{gathered} P(460)=20,950\cdot e^(0.0075\cdot460) \\ P(460)=20,950\cdot e^(3.466) \\ P(460)=20,950\cdot32 \\ P(460)=670,400 \end{gathered}`

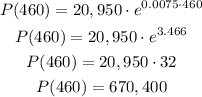
The population 460 years from now will be 670,400.