The free body diagram of the system is shown as,
According to free body diagram,
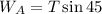
The frictional force can be given as,
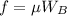
According to free body diagram,
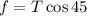
Plug in the known values,
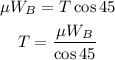
Substitute the known value in above condition,
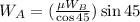
Substituting values,
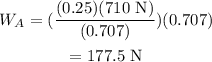
Therefore, the maximum weight of block A for which system will be in equilibrium is 177.5 N.