1. if you use 1/2 cup of sugar, you need 3/4 cup of flour. To find how many cup of flour do you need for 4 cups of sugar, you can use the next proportion:
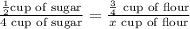
Solving for x
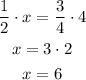
You need 6 cups of flour for the first recipe.
Replacing x = 4 into the equation, we get:
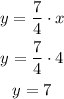
You need 7 cups of flour for the first recipe.
2. The constant of proportionality of the table is got dividing the values of the variables. Taking for example, 1/2 cup of sugar and 3/4 cup of flour,
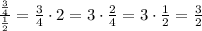
the constant is 3/2 for the first recipe.
In the second recipe, the constant is 7/4; as can be seen in the equation
The constant relates the number of flour cups needed for 1 cup of sugar