Question

asked Aug 6, 2023 33.6k views

1 Answer

Maeh · Answer 1 · 2023-08-10T23:26:42+0000

To prove a biconditional statement we have to prove two conditionals.

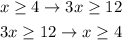
$\begin{gathered} x\ge4\rightarrow3x\ge12 \\ 3x\ge12\rightarrow x\ge4 \end{gathered}$

Let's prove the first one.

$x\ge4$

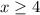
We multiply the inequality by 3.

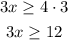
$\begin{gathered} 3x\ge4\cdot3 \\ 3x\ge12 \end{gathered}$

Which proves the first conditional.

Let's prove the second conditional.

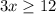
$3x\ge12$

We divide by 3 the inequality.

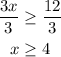
$\begin{gathered} (3x)/(3)\ge(12)/(3) \\ x\ge4 \end{gathered}$

Which proves the second conditional.

Therefore, we can say that the given biconditional statement is true.

The inverse of the biconditional statement would be

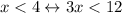
$x<4\leftrightarrow3x<12$

To prove the inverse, we demonstrate each conditional.

$\begin{gathered} x<4\rightarrow3x<12 \\ 3x<12\rightarrow x<4 \end{gathered}$

Let's prove the first conditional.

We multiply by 3 the inequality.

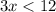
Which proves the first inequality.

Let's prove the second conditional.

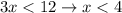
$3x<12\rightarrow x<4$

We divide the inequality by 3.

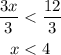
$\begin{gathered} (3x)/(3)<(12)/(3) \\ x<4 \end{gathered}$

Which proves the second inequality.

At last, the contrapositive would be

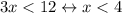
$3x<12\leftrightarrow x<4$

Let's prove it using the same method as the previous ones.

The conditionals we have to prove are

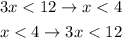
$\begin{gathered} 3x<12\rightarrow x<4 \\ x<4\rightarrow3x<12 \end{gathered}$

First conditional proof.

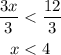
$\begin{gathered} (3x)/(3)<(12)/(3) \\ x<4 \end{gathered}$

Second conditional proof.

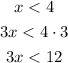
$\begin{gathered} x<4 \\ 3x<4\cdot3 \\ 3x<12 \end{gathered}$