Answer:
y = 1/2 x + 4
Step-by-step explanation:
The slope intercept form of an equation is

where m is the slope and b is the y-intercept.
Now in our case the slope m = 1/2; therefore,
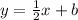
Now we just need to find the value of b.
Luckily we are told that the line passes through the point (-6, 1), which means that the above equation must satisfy x = -6 given y = 1.
Putting in x = -6 and y = 1 in the above equation gives
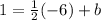
which simplifies to give

adding 3 to both sides gives
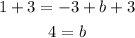
Hence, the value of b is 4, and therefore, our equation becomes
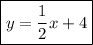
which is our answer!