Question

If a=c(1-s2) how do you express S in terms of A and C

Answer 1

`A=C(1-S^2)`

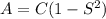
The given equation express A in function of C and S. To express the equation as S in terms of A and C​ you need to solve the variable S:

-Divide both sides of the equation into C

`\begin{gathered} (A)/(C)=(C(1-S^2))/(C) \\ \\ (A)/(C)=1-S^2 \\ \\ \end{gathered}`

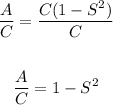
- Substract 1 in both sides of the equation:

`\begin{gathered} (A)/(C)-1=1-1-S^2 \\ \\ (A)/(C)-1=-S^2 \end{gathered}`

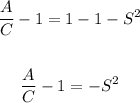
-Multiply both sides of the equation by -1:

`\begin{gathered} (-1)((A)/(C)-1)=(-1)(-S^2) \\ -(A)/(C)+1=S^2 \end{gathered}`

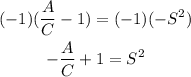
-Take square root of both sides of the equation:

`\begin{gathered} \sqrt[]{(-(A)/(C)+1)}=\sqrt[]{S^2} \\ \\ \sqrt[]{-(A)/(C)+1}=S \end{gathered}`

Then, the equation that express S in terms of A and C​ is:

`S=\sqrt[]{-(A)/(C)+1}`