Answer:
Robbie Glider
Explanation:
Given
Melissa Glider
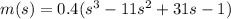
Robbie Glider
See attachment for function
Required
Which reaches the greater maximum within the first 6 seconds
Melissa Glider
First, we calculate the maximum of Melissa's glider
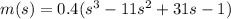
Differentiate:
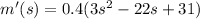
Equate to 0 to find the maximum
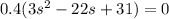
Divide through by 0.4

Solve for s using quadratic formula:
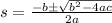
Where

So:

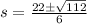
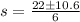
Split:
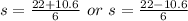
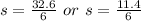
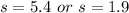
This implies that Melissa's glider reaches the maximum at 5.4 seconds or 1.9 seconds.
Both time are less than 6 seconds
Substitute 5.4 and 1.9 for s in
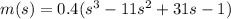 to get the maximum
to get the maximum


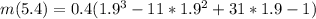
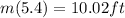
The maximum is 10.02ft for Melissa's glider
Robbie Glider
From the attached graph, within an interval less than 6 seconds, the maximum altitude is at 3 seconds
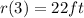
Compare both maximum altitudes, 22ft > 10.02ft. This implies that Robbie reached a greater altitude