Question

You are a member of an alpine rescue team and must get a box of supplies, with mass 3 kg , up an incline of constant slope angle 30.0, so that it reaches a stranded skier who is a vertical distance 4 m above the bottom of the incline. There is some friction present; the kinetic coefficient of friction is 0.05. Since you can't walk up the incline, you give the box a push that gives it an initial velocity; then the box slides up the incline, slowing down under the forces of friction and gravity. Take acceleration due to gravity to be 9.81 m/s2 .What is the minimum speed v that you must give the box at the bottom of the incline so that it will reach the skier

Answer 1

v = 9.04 m / s

Step-by-step explanation:

For this exercise we can use the relation that the work of the non-conservative force (friction) is equal to the variation of the mechanical energy of the system.

W = Em_f - Em₀ (1)

Starting point. Lower slope

Em₀ = K = ½ m v²

highest point. Where is the skier at a height h

Em_f = U = m g h

The work of rubbing

W = -fr x

the negative sign is because the friction force opposes the movement.

Let's set a reference system where the x axis is parallel to the slope and the y axis is perpendicular

let's use trigonometry to break down the weight

cos θ = W_y / W

sin θ = Wₓ / W

W_y = W cos θ

Wₓ = W sin θ

Y axis

N - Wₓ = 0

N = mg sin θ

X axis

fr = m a

the friction force has the expression

fr = μ N

fr = μ mg sin θ

we look for the job

W = - μ mg sin θ x

where x is the distance along the slope

we substitute in 1

-μ mg sin θ x = mg h - ½ m v²

let's use trigonometry to find the distance x

tan 30 = h / x

x = h / tan 30

we substitute

-
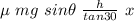`\mu \ mg \ sin \theta \ (h)/(tan 30) \ x` = m gh - ½ m v²

we use

tan 30 = sin30 / cos30

v² = 2g h + 2 μ g h cos 30

v =
`√( 2gh \ (1+ cos 30)`

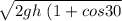
let's calculate

v =
`√( 2 \ 9.8 \ 4 \ (1 + 0.05 \ cos \ 30))`

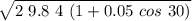
v = 9.04 m / s