Question

Sydney is in the business of manufacturing phones. She must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. Let C represent the total cost, in dollars, of producing p phones in a given day. A graph of C is shown below. Write an equation for C then state the y -intercept of the graph and determine its interpretation in the context of the problem.

Answer 1

The equation of a line in slope-intercept form, is given by:

`y=mx+b`

Where m represents the slope of the line, which is the rate of change of y with respect to x, and b represents the y-intercept of the line, which is the initial value of y when x=0.

If we use C to represent the vertical axis and p for the horizontal axis, then:

`C=mp+b`

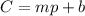
From the data on the graph, we can see that C=200 when p=0. Then, the initial value is 200, then:

`b=200`

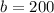
On the other hand, C=250 when p=1. Substitute this information in the equation to find the value of m:

`\begin{gathered} C=mp+200 \\ \Rightarrow250=m(1)+200 \\ \Rightarrow m=50 \end{gathered}`

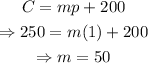
Therefore:

`C=50p+200`

Since Sydney pays for the building and equipment regardless of the number of manufactured phones, then the initial value represents the rent of that building and equipment.

The y-intercept of the function is 200, which represents the rent of the building and equipment, or the cost of producing 0 phones.