Question

For which system of inequalities is (-3, 1) a solution?x + y < -22x – 3y <-9x + y = -2O 2x – 3y <-9x + y<-2• 2x – 3y <-9x + y < -22x – 3y <-9

Answer 1

`\begin{gathered} x+y\leq-2 \\ 2x-3y\leq-9 \end{gathered}`

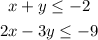
Explanation;

Given the solution of the system of inequalities to be (-3, 1), let's go ahead and substitute x = -3 and y = 1 into each of the given system of inequalities to determine the correct one.

Let's pick the 1st one;

`\begin{gathered} x+y<-2 \\ 2x-3y<-9 \\ put\text{ x = -3 and y = 1 for the 1st inequality} \\ -3+1<-2 \\ -2<-2 \\ \end{gathered}`

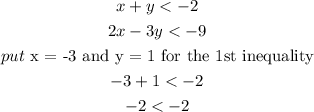
Since -2 is not less than -2 so the 1st system of inequalities is not the correct one.

Looking at the bottom left one, we can see that x + y < -2 is part of the inequalities which had been solved already, so the bottom left system of inequalities is also incorrect.

Let's pick the bottom right one;

`\begin{gathered} x+y\leq-2 \\ 2x-3y\leq-9 \\ \text{put x = -3 and y = 1 in the 1st one} \\ -3+1\leq-2 \\ -2\leq-2 \\ do\text{ same for the 2nd one} \\ 2(-3)-3(1)\leq-9 \\ -6-3\leq-9 \\ -9\leq-9 \end{gathered}`

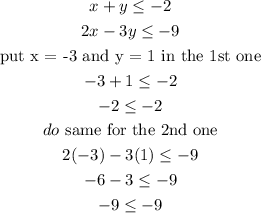
The above system of inequality is the correct one since -2 is equal to -2 and -9 is equal to -9.