ANSWER:
0.839 milliTeslas
Explanation:
Given:
Current (I) = 51.471 A
Distance (d) = 1.227 cm = 0.01227 m
Current solenoid (Is) = 16.358 A
Distance solenoid (ds) =65.271 cm = 0.65271 m
A sketch of the situation:
We calculate the magnetic field for each case:

Therefore, the resulting field due to the wire and the solenoid would be:
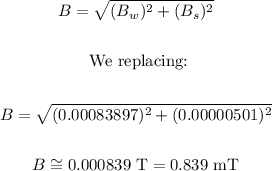
The correct answer is 0.839 milliTeslas