Question

A particle moves along the x-axis so that its position at time 1 is given by x(t) = t^2 - 6t + 5. For that value of t is the velocity of the particle zero?(A) 1(B) 2(C) 3(D) 4(E) 5

Answer 1

Position and Velocity

If we are given the function of the position X(t) where t is the time, the velocity function v(t) is the first derivative of X(t).

The position of the particle is given by:

`X(t)=t^2-6t+5`

The velocity is calculated by finding the first derivative:

`\begin{gathered} V(t)=X^(\prime)(t) \\ V(t)=(t^2-6t+5)^(\prime) \end{gathered}`

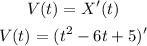
Taking the derivative:

`V(t)=2t-6`

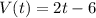
Now we need to find when the velocity is 0, so we equate the function to 0 and solve for t.

2t - 6 = 0

Adding 6:

2t = 6

Dividing by 2:

t = 3

Answer: (C) 3