Answer:
Ns/Np = 0.171
Step-by-step explanation:
First, we will find the ratio of lengths of each wire:
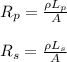
where,
Rs = Resistance of secondary coil
Rp = Resistance of Primary Coil
ρ = resistivity of copper
Ls = Length of the secondary coil
Lp = Length of theprimary coil
A = Area of cross-section of wie
Since the material and wire are the same. Therefore, dividing both equations, we get:
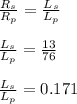
The number of turns are given as:
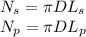
where,
Ns = No. of turns in the secondary coil
Np = No. of turns in the primary coil
D = Diameter of circular turns
D is the same for both coils. Therefore, dividing both equaions:
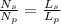
Ns/Np = 0.171