Answer:
Solution Given:
let ABC be an equilateral triangle with the vertex A(2,-1) and slope =-1.
and
∡ABC=∡BAC=∡ACB=60°
slope of BC
![[ m_1]=-1](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/b7b7sbgevvgapof45bmr.png)
we have
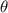 =60°
=60°
Slope of AB=
![[ m_2]=a](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/zmyx9uifjjcwee4dd9fo.png)
now
we have
angle between two lines is
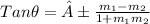
now substituting value
tan 60°= ±
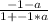
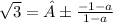
doing criss-cross multiplication;
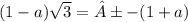
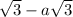 =±(1+a)
=±(1+a)
taking positive
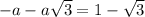
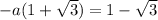
a=
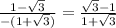
taking negative
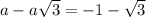
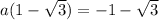
a=
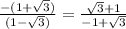
Equation of a line when a =
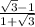
and passing through (2,-1),we have
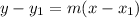
y+1=
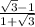 (x-2)
(x-2)
y=
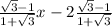 -1
-1
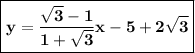 is a first side equation of line.
is a first side equation of line.
again
Equation of a line when a =
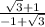
and passing through (2,-1),we have
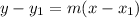
y+1=
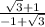 (x-2)
(x-2)
y+1=
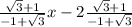
y=
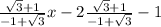
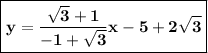 is another equation of line.
is another equation of line.