The z-score formula is
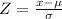
Where μ is the mean and σ is the standard deviation.
Thus, in our case, setting x=0.9
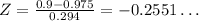
Using a z-score, table,
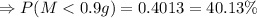
The probability is 0.4013
Since the sample size is greater than 30, we can use the first formula above.
On the other hand,
![Z=\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/college/hxw4zfi6uvrpx1yrz9be89rnherkl1e02q.png)
Then,
![\begin{gathered} \Rightarrow Z=\frac{0.9-0.975}{\frac{0.294}{\sqrt[]{50}}}=-1.80384\ldots \\ \Rightarrow P(M<0.9)=0.0359 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8dewktzfdpmgspyujidnmeduap8slicdeg.png)
In that case, the probability is 0.0359