The given function is:
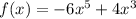
Even functions are unchanged when reflected over the y-axis, so:
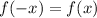
Odd functions are unchanged when rotated 180° about the origin, so:
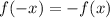
Now, replace -x as the argument of the function and let's observe the result:
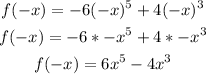
As can be observed, f(-x) is not equal to f(x), then this is not an even function.
Now, let's evaluate -f(x):
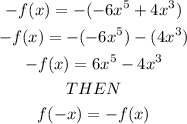
This function is odd.