We know that:
- the original sample was 400 grams
- the half-life (t1/2) is 9 hours
And we must find how many grams of the imaginary element 317-Bulldogs will be left after 45 hours.
To find it, we need to know that
And to determine the amount of a radioactive isotope remaining after a given number half-lives we can use the next formula:
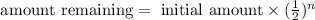
Where n is the number of half-lives.
Now, to use the formula we need calculate n
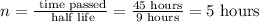
Then, having that n = 5 we can replace the values in the formula for the amount remaining
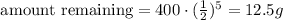
ANSWER:
There would be 12.5 grams left of 317-Bulldogs after 45 hours