The equation of a line is given as:
y = mx + c
Let us get the eqiuations for the first two sets of data points
( 1, 5) and (2, 2)
For (1, 5), the equation becomes:
5 = m + c
m + c = 5........(1)
For (2, 2), the equation becomes:
2 = 2m + c
2m + c = 2........(2)
Subtract equation (1) from (2)
m = -3
Put the value of m into equation (1) to get the value of c
-3 + c = 5
c = 5 + 3
c = 8
The general equation then becomes:
y = -3x + 8
To confirm that this function is right, put the third data point into the equation and see if it is true.
(3, -1)
-1 = -3(3) + 8
-1 = -9 + 8
-1 = -1 (true)
To find the inverse of the function y = -3x + 8
Make x the subject of the formula
-3x = y - 8
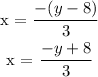
To get the inverse function, replace x by y, and vice-versa

We will now use the values of y in the first table as x in the inverse function table:
when x = 5
y = (-5 + 8)/3
y = 3/3, y = 1
When x = 2
y = (-2 + 8)/3 = 6/3
y = 2
When x = -1
y = (-(-1) + 8) / 3 = (1 + 8)/3
y = 9 / 3
y = 3
The table for the inverse function is therefore:
Below is the graph for the original function:Below is the graph for the inverse function: