Consider the schematic diagram given below,
In the diagram, AB represents the height of the tree, and point C is the location of the observer.
The angle of of elevation to the top of the tree is the angle BCA here.
This angle can be calculated as,
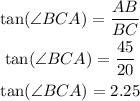
Taking the inverse function both sides,
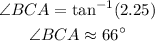
Thus, the required angle of elevation is approximately 66 degrees.