Question

Find the value of k so that (x^4-2x^2+kx+6) is divided by (x-2) , the remainder is 0.

Answer 1

To solve this questio, we have to divide the given polynomial by the binomial as normal:

At this point, we have to continue with the division:

For the last term of the quotient we use the following reasoning: We need a number that when multiplied by -2 the result is 6, that way the remainder will be 0. That number is -3. When multiplying -3 by x we obtain -3x. It means that (2+k)x has to be equal to -3x. Use this information to find the value of k:

`\begin{gathered} (2+k)x=-3x \\ 2+k=-3 \\ k=-3-2 \\ k=-5 \end{gathered}`

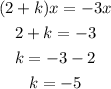
It means that k has a value of -5.