Answer:
Explanation:
The dimensions of the rectangular prism are:
• Length = 5in.
,
• Width = 4/5 in.
,
• Height =1 3/5 in.
The cube has a side length of 1/5 inches.
The number of cubes to pack the prism is determined using the formula below:
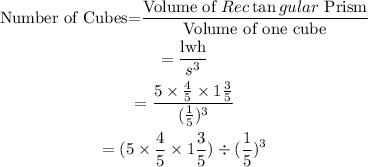
The operation is simplified below:
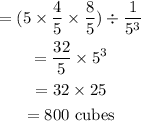
800 cubes are required to completely pack the prism without any gap or overlap.