Question

A motorboat travels 210 miles in 6 hours going upstream. It travels 330 miles going downstream in the same amount of time. What is the rate of the boat instill water and what is the rate of the current?Note that the ALEKS graphing calculator can be used to make computations easier.

Answer 1

Distance travelled by the motorist going upstream = 210 miles

Time travelled = 6hours

Distance travelled by the same motorist going downstream = 330 miles

Time travelled = 6 hours

Let x miles per hour represent the rate of the boat in still water

Let y represent the rate of the current

Since the rate of the boat in still water is represented by x, but from the question, the boat is not in still water but travelling upstream and downstream.

If the boat is travelling upstream, the current will push against the boat and the speed will decrease.

Therefore, the resulting speed of the boat will be (x - y)miles per hour.

However, If the boat is travelling downstream, the current pushes it faster and there will be an increase in the boat's speed

Therefore, the resulting speed of the boat will be (x + y) miles per hour.

Relation between distance, rate and time is given by:

`\text{ Distance = Rate x Time}`

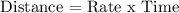
On travelling upstream

`\text{ 210 = 6}(x-y\text{)}`

On travelling downstream

`330=6(x+y)`

We now solve both equations simultaneously, using the elimination method

`\begin{gathered} 210=6x-6y\ldots\ldots(1) \\ 330=6x+6y\ldots\ldots(2) \\ \text{Subtract equation (1) from (2)} \\ 330-210\text{ = 6}y-(-6y) \\ 120=12y \\ y=(120)/(12)=10 \end{gathered}`

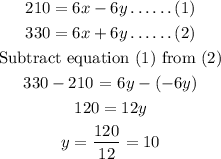
In order to find x, substitute y= 10 into equation (1)

`\begin{gathered} 210=6x-6(10) \\ 210=6x-60 \\ 210+60\text{ = 6}x \\ 6x=270 \\ x=(270)/(6)=45 \end{gathered}`

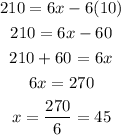
Hence, the rate of the boat in still water and the rate of the current are 45 miles per hour and 10 miles per hour