Given:
Required:
We need to find the rate of the amount of water in the pool and the amount of water in the pool before Bill adds water to the swimming pool.
Step-by-step explanation:
a)
Consider the amount of water in the pool at different amounts of time.
112 gallons, 148 gallons, 184 gallons, and 220 gallons.
We know that
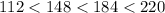
The amount of water is increasing.
We get the points (6,112) and (9, 148) from the table.
The rate of change formula is

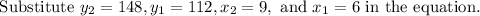
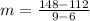
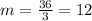
As the time increases, the amount of water in the pool is increasing
12 gallons per minute of water in the pool is increasing.
b)
The rate is constant.
Consider the function equation.
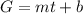
Here m is the rate of water in the pool increasing, b is the amount of water in the pool before Bill adds water to the swimming pool, and G s the amount of water in the pool at time t.
Substitute m=12, t=6, and G =112 in the equation to find the value of b.
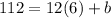
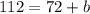
Subtract 72 from both sides.
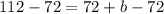
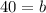
40 gallons of water in the pool before Bill adds water to the swimming pool.
Final answer:
a)
As the time increases, the amount of water in the pool is increasing
12 gallons per minute of water in the pool is increasing.
b)
40 gallons of water in the pool before Bill adds water to the swimming pool.