Question

If y = x² + kr - k, for what values of k will the quadratic have two real solutions?

Answer 1

The given expression is

`y=x^2+kr-r`

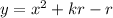
Where a = 1, b = 0, and c = kr-k.

Let's use the discriminant

`\begin{gathered} D=b^2-4ac \\ D=0^2-4\cdot1\cdot(kr-r) \\ D=-4kr+4r \end{gathered}`

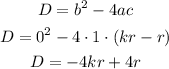
It is important to know that the equation has two real solutions when the discriminant is greater than zero, so

`-4kr+4r>0`

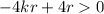
Let's factor out the greatest common factor

`4r(-k+1)>0`

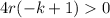
Now, we solve for k.

`\begin{gathered} -k+1>(0)/(4r) \\ -k+1>0 \\ -k>-1 \\ k<1 \end{gathered}`

Hence, k must be less than 1 in order to have two real solutions.