Given the graph of the rational function:
As shown there are two asymptotes
The lines of the asymptotes are:
x = -3, x = 2
So. the factors of the denominator are:
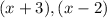
Note: (x - 2) will be repeated
And the function has an x-intercept at the point x = 1
So, the factor of the numerator will be (x - 1)
So, the function will have the following form:
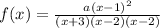
we will find the value of (a) using the point of the y-intercept
As shown the y-intercept = (0, -1/2)
So, substitute with x = 0, f = -1/2
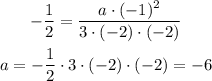
So, the answer will be:
The numerator is: -6 (x - 1)²
The denominator is: ( x + 3) ( x - 2 ) (x - 2)