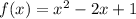A quadratic equation can be written in the vertex form to be:
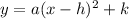
where (h, k) is the vertex.
The question gives the following parameters:
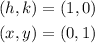
We can use these values to solve for a:
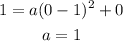
Therefore, the vertex form of the quadratic equation will be:
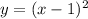
Expanding, we have the general form of the quadratic equation to be: