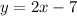First, let's solve the system:
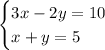
Clearing y from equation 2, substituting in equation 1 and solving for x :

Substituting and solving for y :
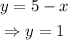
We get that the solution for the system is:
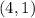
In order for two lines to be parallel, they need to have the same slope. This means that we'll use a slope of 2.
Using this, the point calculated and the slope-point form:
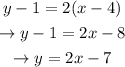
We get that the equation of the line that is parallel to y = 2x+1 and passes through (4 ,1) is: