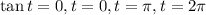To answer this question, we have that we need to find the values for t where the tangent function will be equal to zero.
We have that:
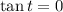
And, if we see that the function tangent is equal to:
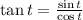
We need to find, in the interval:
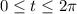
The values for which sin(t) = 0. If we see the unit circle, the points, in this interval, where sin(t) = 0 are t = 0, t = pi, and t = 2*pi.
Therefore, we have that the points for tan(t) = 0 are, therefore (in the given interval):