Question

Use the real zeros to factor f over the real numbers

Answer 1

A. x = 2, √11, -√11

Step-by-step explanation

To find the zeros of f, which is a 3rd-degree polynomial, we can try some common values to see if any of them is a zero: 1, 2, -1, -2. In this case 2 is a zero of the function:

`\begin{gathered} f(2)=2\cdot2^3-4\cdot2^2-22\cdot2+44 \\ f(2)=2\cdot8-4\cdot4-44+44 \\ f(2)=16\cdot16 \\ f(2)=0 \end{gathered}`

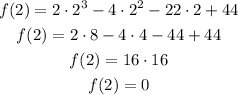
Now we can reduce our polynomial by dividing it by the factor (x - 2) and obtain a 2nd-degree polynomial, whose zeros are easier to find:

So we can rewrite f(x) as:

`f(x)=(x-2)(2x^2-22)`

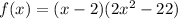
To find the other two zeros we have to solve:

`2x^2-22=0`

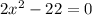
Add 22 to both sides of the equation:

`\begin{gathered} 2x^2-22+22=0+22 \\ 2x^2=22 \end{gathered}`

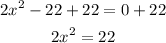
Divide both sides by 2:

`\begin{gathered} (2x^2)/(2)=(22)/(2) \\ x^2=11 \end{gathered}`

And take square root. Remember that the square root has a positive and a negative result:

`\begin{gathered} \sqrt[]{x^2}=\pm\sqrt[]{11} \\ x=\pm\sqrt[]{11} \end{gathered}`

So the other two zeros are √11 and -√11.

The three real zeros of f are 2, √11 and -√11