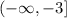Domain: Set of x-values for which the function is defined.
The given function is a quadratic function, the quadratic functions are defined for all values of x.
The domain of the given quadratic function is:
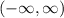
________________________
Range: Set of y-values that takes the function.
To identify the range of a quadratic function you need to find the vertex and identify if the parabola opens up or down.
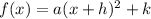
The given function is written in the vertex form. The coordinates of the vertex are (h,k).
A parabola opens up if a>0
A parabola opens down if a<0
Given function:
a= -4. The parabola opens down
Vertex: (-1,-3)
As the parabola opens down the y-coordinates of the vertex is the maximum value of the function (parabola goes from y = -∞ to y= -3)
The range of the given quadratic function is: