SOLUTION
Step 1: Let us draw a pictorial view of the information given:
The height of the antenna AB will be:
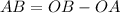
Let us find OA from triangle OAS
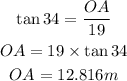
Now, we will find OB from triangle OBS
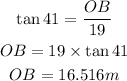
Now, let us find length AB, which is the length of the antenna:
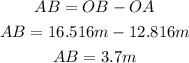
The height of the antenna is 3.7 meters.