Question

Can we make this quick I gotta have this question done really quick thank you

Answer 1

The given problem can be exemplified in the following diagram:

In the diagram we have the following forces:

`\begin{gathered} F=\text{ pushing force} \\ F_x=\text{ x-component of the force} \\ F_y=\text{ y-component of the force} \\ N=\text{ normal force} \\ F_f=\text{ friction force} \\ W=\text{ weight} \end{gathered}`

Now we will determine the value of the acceleration of the box. To do that we will add the forces in the horizontal direction:

`\Sigma F_h=F_x-F_f`

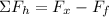
According to Newton's second law we have that the sum of forces must be equal to the product of the mass and the acceleration:

`F_x-F_f=ma`

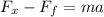
To determine the value of the friction force we use the following relationship:

`F_f=\mu N`

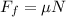
To determine the value of the normal force we add the forces in the vertical direction:

`\Sigma F_v=N-F_y-W`

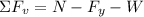
Since there is no movement in the vertical direction we have:

`N-F_y-W=0`

Now we solve for the normal force:

`N=F_y+W`

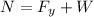
To determine the vertical component of the force we use the right triangle shown in the diagram. We use the function sine and we get:

`\sin 35.7=(F_y)/(F)`

Now we multiply both sides by "F":

`F\sin 35.7=F_y`

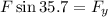
Now we substitute this value in the formula for the normal force:

`N=F\sin 35.7+W`

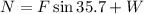
Now we substitute this value in the formula for the friction force:

`F_f=\mu(F\sin 35.7+W)`

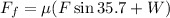
Now we substitute this value in the formula for the horizontal forces:

`F_x-\mu(F\sin 35.7+W)=ma`

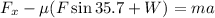
Now, to determine the horizontal component of the force we use the function cosine:

`\cos 35.7=(F_x)/(F)`

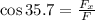
Now we multiply both sides by "F":

`F\cos 35.7=F_x`

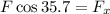
Now we substitute in the sum of horizontal forces:

`F\cos 35.7-\mu(F\sin 35.7+W)=ma`

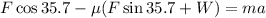
Now we solve for "a" by dividing both sides by "m":

`(F\cos 35.7-\mu(F\sin 35.7+W))/(m)=a`

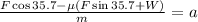
To determine the mass we use the formula for the weight:

`W=mg`

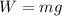
Where:

`g=\text{ acceleration of gravity}`

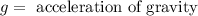
Now we divide both sides by "g";

`(W)/(g)=m`

Now we substitute the values:

`((401N)\cos 35.7-(0.587)(401N\sin 35.7+245N))/((245N)/(9.8(m)/(s^2)))=a`

Solving the operations we get:

`1.779(m)/(s^2)=a`

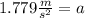
Now, we will determine the final velocity of the movement. We will use the following equation of motion:

`2ad=v^2_f-v^2_0`

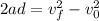
Since the box starts from rest this means that the initial velocity is zero:

`2ad=v^2_f`

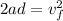
Now we take the square root to both sides:

`\sqrt[]{2ad}=v_f`

Now we substitute the values:

`\sqrt[]{2(1.779(m)/(s^2))(3.37m)}=v_f`

Solving the operations:

`3.46(m)/(s)=v_f`

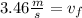
Now we use the following equation of motion to determine the time:

`v_f=v_0+at`

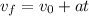
Since the initial velocity is zero:

`v_f=at`

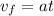
Now we divide by the acceleration:

`(v_f)/(a)=t`

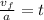
Substituting the values:

`(3.46(m)/(s))/(1.779(m)/(s^2))=t`

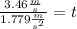
Solving the operations:

`1.94s=t`

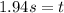
Therefore, it takes the box 1.94 seconds to move.