The given expression is,
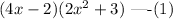
We know, (a+b)(c+d)=a(b+c)+b(c+d).
Hence, applying the above indentity to expression (1),
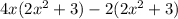
Also, a(b+c)=ab+ac. Applying this identity to the above expression, we get
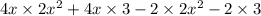
Multiplying the terms,
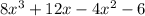
Rearrange the terms.
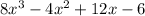
Therefore, the product of the given expression is,
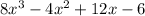
Hence, option (D) is correct.