Given:
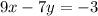
The given equation of the line is written in standard form.
We will write the equation in slope-intercept form, we will solve the equation for (y) as follows:
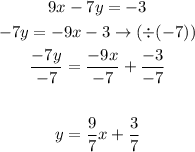
So, the slope of the line = 9/7
We will answer the following questions:
a) What is the slope of a line parallel to this line?
The parallel lines have the same slope
So, the slope of a parallel line = 9/7
b) What is the slope of a line perpendicular to this line?
the product of the slopes of the perpendicular lines = -1
So, we will find the negative of the reciprocal of the given slope
So, the slope of the perpendicular line = -7/9