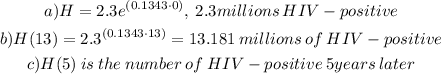
1) In this problem, let's work with an exponential model.
a) To find out how many people were living with HIV infection we're going to consider 1990 as the first year. The year "0"
So we can write out
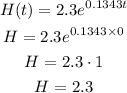
Note that we plugged into t, t=0 then we know that according to that exponential model there were 2.3 million people HIV positive in 1990.
b) Now we can evaluate the function, 13 years later in 2003, so we'll plug into that t=13:
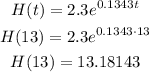
So 13 years later there were more than 13 million people infected
c) In this case, the meaning of H(5) is the number of HIV positive 5 years later since t is given in years. In other words, H(5) is the number of HIV positive in 1995.