Question

Sum of Geometric Series Problem Sn=a+ar+ar^2+...+ar^n-1, S2=3.5, S3=11.375, and r<0. Find a and r.

Answer 1

Sum of Geometric Series

We have that

`\begin{gathered} Sn=a+ar^1+ar^2+...+ar^(n-1) \\ S_2=3.5,S_3=11.375 \end{gathered}`

Now, we have two equations:

`\begin{gathered} a+ar=3.5 \\ a+ar^1+ar^2=11.375 \end{gathered}`

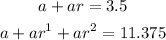
We have that:

`S_n=(a\mleft(1-r^n\mright))/(1-r)`

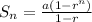
Then, for S2 and S3:

`\begin{gathered} S_2=(a(1-r^2))/(1-r)=3.5 \\ S_3=(a(1-r^3))/(1-r)=11.375 \end{gathered}`

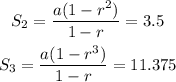
Then, we have two equations:

`\begin{gathered} (a(1-r^2))/(1-r)=3.5 \\ (a(1-r^3))/(1-r)=11.375 \end{gathered}`

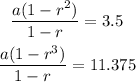
Now, solving for (1 - r):

`\begin{gathered} (a(1-r^2))/(3.5)=1-r \\ (a(1-r^3))/(11.375)=1-r \end{gathered}`

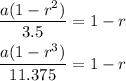
We equate them:

`(a(1-r^2))/(3.5)=(a(1-r^3))/(11.375)`

Now, we can solve for r:

`\begin{gathered} (a(1-r^2))/(3.5)=(a(1-r^3))/(11.375) \\ \downarrow \\ (1-r^2)/(3.5)=(1-r^3)/(11.375) \\ \downarrow \\ 11.375\cdot(1-r^2)=3.5(1-r^3) \end{gathered}`

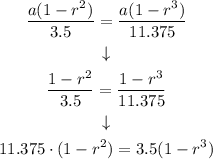
Dividing both sides by 3.5:

`\begin{gathered} 11.375\cdot(1-r^2)=3.5(1-r^3) \\ \downarrow \\ 3.25(1-r^2)=1-r^3 \\ \downarrow \\ 3.25-3.25r^2=1-r^3 \end{gathered}`

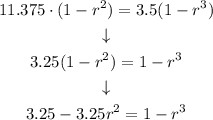
Now, rearraging the equation we have that:

`r^3-3.25r^2+2.25=0`

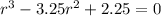
From the equation, we have that r has three possible values:

`\begin{gathered} r_1=3 \\ r_2=_{}1 \\ r_3=-(3)/(4)=-0.75 \end{gathered}`

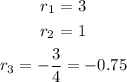
We know this because of the graph of the equation:

Since r < 0, then the solution is:

`r=-(3)/(4)=-0.75`

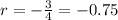
Since

`\begin{gathered} a+ar=3.5 \\ \downarrow \\ a(1+r)=3.5 \end{gathered}`

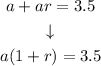
we can find a if we replace r = -3/4:

`\begin{gathered} a(1-0.75)=3.5 \\ a(0.25)=3.5 \end{gathered}`

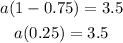
Then,

`a=(3.5)/(0.25)=14`

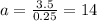
Therefore the values of r and a are:

Answer- r = - 0.75 and a = 14