Question

Graph each function. Then identify the vertex, domain, and range. F(x)= 3|x|-3

Answer 1

The plot of the absolute value function is

Let's start first by getting the domain and range of the given absolute value function

`f(x)=3|x|-3`

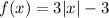
The function will have a corresponding value for any value of x. This means that the domain of the function is all real.

Using the plot as a basis to find the range of the function, the function shows vertex at (0,-3). This means that the function has a value starting from y = -3 up to positive infinity. Hence, the range of the function is

`\text{range}=\lbrack-3,\infty)`

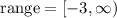
The vertex of the absolute value of the function is the encircled point in the figure below.

Base on the plot, the vertex exists at (0, -3).